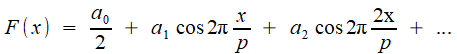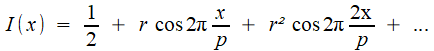Cristallographie, Optique, Astronomie...
... Une Promenade Fouriériste! (Partie 4.3)
Nous poursuivons l'exploration du vaste monde des applications de la transformation de Fourier; dans cette page, on a regroupé tout ce qui touche à l'optique --en un sens assez large, comme on le verra!
Des cristaux aux quasi-cristaux
Émise par Haüy en l'an 1781, l'idée qu'ils sont un empilement d'atomes n'est toujours, au début du XXème siècle, que l'hypothèse la plus probable! D'autant que de nombreux savants en France sont ce qu'on appelerait probablement aujourd'hui des "atomo-sceptiques", dont le très influent Marcelin Berthelot; il faut en revanche saluer ici la clairvoyance d'un Jean Perrin, atomiste convaincu. Pour en revenir à Haüy, il fut le professeur de Fourier; ni l'un, ni l'autre ne pouvaient deviner que bien des années plus tard, leurs noms seraient associés dans l'histoire de la discipline!Ce qu'il faudrait pour donner des preuves, c'est pouvoir faire des mesures de distance éclairantant leur disposition. Deux outils... (et des gens pour les mettre à profit) vont intervenir.
Prélude: outillage physique
La diffraction de la lumière est connue depuis Fresnel : elle résulte de la nature ondulatoire de la lumière (lire une analyse de son mémoire sur BibNum). Lorsque celle-ci traverse une grille fine, l'optique géométrique prédirait une simple ombre portée de la grille, les rayons poursuivant leur route en ligne droite. Mais si la grille est très fine (du même ordre de taille que la longueur d'onde du rayon), les lois de l'optique géométrique cessent de s'appliquer et chaque trou se comporte comme s'il était une nouvelle source luimneuse: la source unique est, en quelque sorte, fractionnée en une multitudes de sources, d'où le nom. C'est le principe de base pour les interférences lumineuses, qui vont être utilisées ià plusieurs reprises dans cette page.Mais... il y a un mais: le phénomène ne peut se produire que si la longueur d'onde de la lumière est inférieure au pas de la grille. Dans l'exploration d'un cristal, c'est le réseau d'atomes qui constitue la grille, et les distance interatomiques (évaluées à l'estime, mais assez correctes) sont inférieures à toutes les longueurs d'onde alors connues dans le spectre.
 |
 |
|
exemple de diffraction dune source lumineuse par une grille:
démonstration par Sylvain Ravy lors d'une conférence |
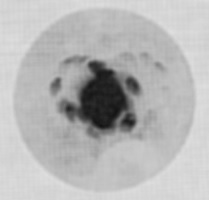
Les Rayons X ont été déccouvert en 1895 par Wilhelm Röntgen (incidemment, savez vous que son cousin Julius était un compositeur de talent, dont la musique vous pénétrait jusqu'à la moëlle des os, disait Grieg?). Ils lui ont valu le prix Nobel 1901; leur longueur d'onde les rend susceptibles d'être diffractés par le réseau cristallin... il n'y a plus qu'à monter l'expérience. Max Von Laue a des idées pour cela, et des complices: ...Friedrich, assistant de Sommerfeldt, et Knipping, doctotrant de Röntgen. Sauf que le patron du laboratoire -Sommerfeldt, justement!- ne veut pas, et qu'ils devront attendre une de ses absences pour tenter et réussir l'expérience, en avril 1912. Il s'agit d'observer sur un écran les interférences des rayons X diffractés par un cristal. L'interprétation de Von Laue est erronnée (fluorescence), mais l'avancée lui vaudra le Nobel 1914.
 |
 |
| premier cliché de diffraction X, repris par un timbre à la gloire de l'auteur de la méthode. |
|
Fourier entre en scène
L'interprétation correcte viendra de William H. Bragg (1862-1942) et William L. Bragg
(1890-1971), son fils. Ce dernier énonce la loi éponyme; elle est basée
sur un mini-calcul géométrique de la différence de chemin entre deux
rayons réfléchis par des atomes situés dans des plans différents
distants de d : leur
interférence sera constructive si la différence de marche est un
multiple entier de la longueur d'onde (en ce cas, la lumière est
maximale par somme des amplitudes); les parties noires correspondant à
des ondes en opposition de phase: rien de nouveau depuis Fresnel!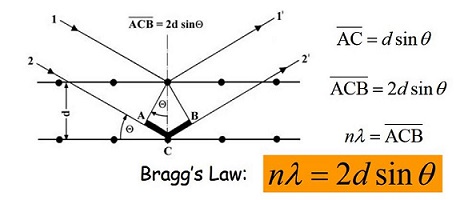 |
"Cette relation est connue comme loi de Bragg, et jai toujours trouvé que l'associer à mon nom était un honneur bien facilement gagné, puisqu'il s'agit simplement d'une relation usuelle en optique pour la réflexion sur des films minces, présentée sous une autre forme." W.L. Bragg
|
Ensuite, il a le génie d'inverser la recherche de Laue: celui-ci voulait aller des cristaux vers les figures de diffraction, Bragg comprend qu'il doit pouvoir remonter des figures de diffraction aux cristaux, c'est à dire exploiter les premières pour comprendre la structure interne des seconds.
C'est, en revanche, son père qui le premier (1915), relie ce travail à l'analyse de Fourier:
 |
|
| la première page de la Bakerian Lecture de Bragg, et le passage crucial |
|
100 ans( plus si on se rapporte à la
présentation à l'Académie, un peu moins si l'on prend pour base la
publication) après Fourier, Bragg a compris -et fait savoir -que le
travail de maturité de l'ex-élève Fourier peut apporter une aide énorme
aux classifications de son ex-professeur Haüy!
Du Sel de Cuisine à l'ADN
Dès 1913, les Bragg élucident plusieurs sructures: le sel ordinaire
(NaCl), la blende (ZnS), le diamant... et encore un prix Nobel dans
cette page! (1915, père et fils). Mais leur investigation atteint
rapidement ses limites: ils trouvent parce qu'ils ont une idée
approximative de ce qu'ils cherchent. Ainsi, la structure du diamant
avait été conjecturée 30 ans auparavant par William Barlow (1845 - 1934), un géologue parvenu aux mêmes idées de classification que le chimiste Fédorov, dans son article Probable Nature of the Internal Symmetry of Crystals. (Nature 1883, n°29). |
 |  |
| source: exposition Cristallography (pour les 100 ans de la diffraction des rayons X). et à part ça, puisque... les diamants intéressent du monde, offrez vous un petit plaisir pas cher: quelques minutes d'une éblouissante Marylin!
|
||
À partir de 1925, chimistes et
cristallographes utilisent les séries de Fourier pour analyser des
structures de plus en plus complexes (de vrais objets 3D, terriblement
"tordus"!); pénicilline et cholestérol en sont des exemples
typiques, dont l'importance médicale est évidente. Et c'est là que,
bien avant son emploi dans l'imagerie radiologique, le transformation
de Fourier allait servir la cause d'Esculape... lentement, certes, mais
tout de même en s'appuyant sur un système d'économie des calculs, c'est à dire la même philosophie que celle de la FFT.
Les bandes de Beevers-Lipsons firent même un peu de résistance à l'arrivée de la FFT
(1965), puisqu'elles furent utilisées jusqu'en 1971. Toutefois, dès les
années 50, l'opérateur s'aidait d'une machine à claculer mécanique pour
les sommes. Une utilisatrice particulièrement célèbre du couple gagnant
(rayons X, bandes de Beevers-Lipsons) est la chimiste britannique Dorothy Hodgkin : elle découvrit la structure du cholestérol en 1937, de la pénicilline pendant la seconde guerre mondiale (publié en 1945), de la vitamine B12 en 1954 et de l'insuline en 1969 et fut la troisième femme, lauréat du prix Nobel de Chimie (1964).
|
"L'un de nous (C.A.B.) suggéra alors d'essayer la méthode de Fourier récemment proposée par Bragg. Bragg l'avait testée sur une structure connue, le diopside, mais personne ne s'en était jamais servi pour une structure inconnue.
Il y avait cependant deux difficultés: nous ne disposions pas de
mesures quantitatives et n'avions aucune expérience dans la sommation
de séries de Fourier à deux variables, bien que nos cours de
mathématiques nous aient fourni une expérience considérable dans la
sommation des séries à une variable. Travailler sur des sommes partielles de 90 termes en deux variables était une autre paire de manches!
Le département de Manchester vint à notre aide pour le premier problème [...]"
|
|
bandes de Beevers-Lipson
source: Wikipedia et Musée des Sciences d'Oxford |
"Dans le cas du pentahydrate de sulfate de cuivre, environ 90 plans participaient à l'évaluation. Divisant les axes x et y
en, disons 60 et 30 parties respectivement, il fallait calculer les
sommes en 1800 points. La méthode la plus immédiate était de calculer hx+ky, prendre le cosinus, multiplier par Fh,k et sommer les 90 valeurs à chacun des 1800 points. Des additions aussi longues sont excessivement pénibles, surtout quand il faut les faire de tête; il y avait donc une forte motivation pour réduire ces additions. Le matin du 4 Décembre 1933, l'un de nous (H.L.) suggéra qu'il serait bien plus avantageux de développer cos (hx+ky) selon la formule bien connue cos hx cos ky - sin hx sin ky.
Bien que cela pût sembler aggraver les choses au premier coup d'œil,
dans la mesure où il fallait maintenant ajouter deux termes au lieu
d'un seul, cela rendit en fait le calcul bien plus facile. Pour
chaque valeur de h, on pouvait sommer les Fh,k cos ky pour tous les y, et ultérieurement employer cette somme comme coefficient des valeurs cos hx. Pour chaque valeur de h, la somme ne portait plus que sur 2k nombres au lieu de hk. [...] Les valeurs de A. cos hx et B. sin hx peuvent être imprimées sos formes de tables, puis coupées en bandes, en sorte que la sommation de Fourier consiste simplement en la sélection des bandes appropriées posées les unes en dessous des autres, puis additionnées pour fournir les différents sous-totaux. Des tables séparées sont constituées pour chaque valeur de h, avec les valeurs de x en lignes et A en colonnes. " C.A. Beevers, H. Lipson
|
Il y a encore un petit trick à assimiler... n'avez vous pas été surpris par l'évocation de calculs faits de tête, alors que les fonctions trigonométriques ont des valeurs bien compliquées? Regardez mieux les bandes ci-contre: elles ne comportent que des nombres entiers. En fait, la table des A . cos hx, ou plutôt, dans la réalité, la table des A . cos (2πhx / 60) ne contenait que des valeurs arrondies aux entiers. Les intervalles, également par pas entiers, étaient:
|
 |
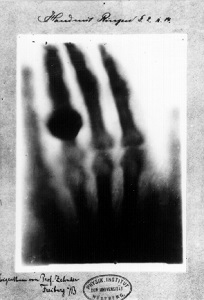
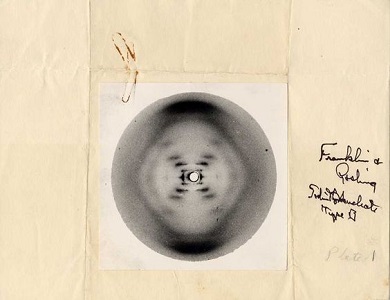
Le cas de la découverte de l'ADN est lui aussi intéressant: en 1952, Francis Crick avait montré que la transformée de Fourier d'une hélice est une croix en pointillés. Et c'est exactement ce que Rosalind Franklin fut la première à observer en 1953, sur les clichés qu'elle réalisa. James Watson et Francis Crick, qui reçurent le prix Nobel en 1962, la remercièrent de leur avoir fourni ces précieuses images, encore non publiées... ce qui était bien le moins qu'ils pouvaient faire, Crick les lui ayant carrément dérobés à son insu, pour les montrer à un Watson qui se plaignait de n'avoir pu soutirer la moindre information à la chercheuse! Une injustice qui transforma la "Dame du côté obscur de l'ADN" en icône de l'oppression des femmes.
ci-contre, un cliché originale de R. Franklin
|
 |
|
 |
Un petit peu de technique: pourquoi une croix de Saint-André? L'encadré ci-contre, tiré de l' article
De la simple hélice aux nanostructures tubulaires (dans la revue de la SFP, Reflets de la physique, n°44-45), vous l'explique dans les grandes lignes. Il est bon de savoir au préalable ce qu'est la "fonction" ð de Dirac, et que la transformation de Fourier échange ð et 1; nous vous l'avons présentée dans la page Naissance de la Transformée de Fourier. (Cadre à agrandir en cliquant!) |
La cristallographie avait ainsi offert sa plus puissante technique aux chimistes et biochimistes. Pour la découverte de la structure du ribosome en 2000 (prix Nobel 2009), les bandes de papier étaient remisées depuis longtemps, et les ordinateurs tournaient à plein régime!
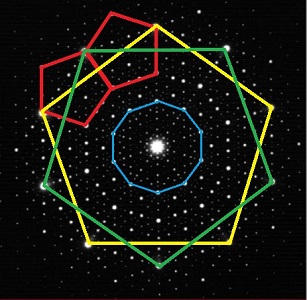
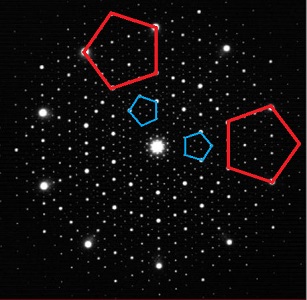
C'est parce que les figures de diffraction réalisent naturellement une transformation de Fourier que la structure elle-même devient accessible par transformée de Fourier inverse. On peut, dans certains cas, se "contenter" de la transformation directe naturelle pour apprendre des choses étonnantes, voire déroutantes: c'est le cas de la découverte des quasi-cristaux (1982) par Dan Shechtman (prix Nobel 2011). De façon générale, la figure de diffraction hérite des propriétés de symétrie du cristal de base; la surprise fut d'y découvrir des symétries pentagonales et décagonales dont l'impossibilité était bien démontrée dans les réseaux cristallins.
Pour en savoir plus sur cette passionnate histoire, et retrouver son anticipation médiévale à Isfahan (Iran), rendez- vous sur notre page dédiée!
Les Débuts de l'Optique de Fourier
|
"J’avais un peu étudié la transformation de Fourier à Bordeaux, pendant le premier trimestre de l’année scolaire 1918-1919, au cours d’Analyse Supérieure du Professeur Cousin, à la demande de mon chef militaire, le Professeur Henri Bénard. Celui-ci me fit appliquer les équations de Fourier à la mesure de coefficients de conductibilité thermique par la propagation en régime variable. Ce fut ma première publication scientifique. J’y parlais de Fourier : j’étais visiblement prédestiné, mais quand je le retrouvais 15 ans plus tard, je l’avais complètement oublié."
P.M. Duffieux, Comment j’ai pris contact avec la transformation de Fourier
|
 l'édition Masson 1970...
|
 ... et son auteur |
C'est un livre publié à compte d'auteur en 1946 qui marque le début de ce que l'on appellera bientôt Optique de Fourier.Il est difficile d'être moins explicite que son titre! L'auteur, Pierre Michel Duffieux (1891 – 1976), normalien (1912), en avait exposé les idées dès 1941, mais s'était heurté à une incompréhension totale de l'auditoire:
|
|
| Tandis qu'il menait une carrière "ordinaire" de professeur à l'université à Besançon -qui a depuis donné son nom à un laboratoire d'optique- Max Born et Emil Wolf attirèrent l'attention sur cet ouvrage dans leur célèbre Principles of Optics (1959). Ce qui lui permit d'être enfin édité en France (Masson, 1970), puis traduit en Anglais (1983). | |||
|
"Mais
en 1934 Fabry m’avait dit : "Ostwald utilise la formule de Van Cittert
pour les corrections des défauts de planéité de ses lames
d’interféromètre. Je l’ai essayée jadis, elle ne vaut rien". Elle consistait à remplacer le cosinus de la formule des franges:
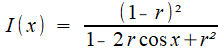 P.M. Duffieux, op. cit.
|
|
"Au
milieu de novembre [...], j’ai envoyé une note avec deux équations
l’une en sinus, l’autre en cosinus, donnant : la première la condition
de parallélisme optimum, l’autre la position des plans parfaits que
l’on pouvait substituer aux surfaces réelles, avec toutes les
corrections accessoires désirables. Le surlendemain matin, Fabry me
téléphona à Rennes : «Qu’est-ce que
c’est que ces équations ? où les avez-vous trouvées ? Je ne les
comprends pas et aucun des opticiens que je connais n’en voudra.
Trouvez autre chose, mais ça non ; ça ne passera jamais à la Revue
d’Optique» .
|  |
|
J’allais
dans mon amphithéâtre vide, qui avait un long tableau noir et 36 places
assises pour 70 [étudiants]; les autres s’asseyaient, les jambes
pendantes, sur la galerie haute qui courrait sur trois côtés et servait
au garçon à ouvrir et fermer mes six fenêtres. J’écrivis mes deux
équations sur le tableau, je m’assis en face et je les regardai. Dieudonné vint me voir pour raisons de service.
«Qu’est-ce que vous faites de ces équations ? - Je m’en suis servi pour étudier les aberrations des franges du Michelson et Fabry me demande où je les ai trouvées et qu’est-ce que c’est. - Mais ce sont les équations de la transformation de Fourier, série, et réduites au premier terme !».
C’était vrai, et à travers 15 ans d’abandon je revis le cours de Cousin de 1918. Je pardonne à Dieudonné son mépris pour Euclide et son cri de guerre nicéen : «Mort au triangle!» ."
P.M. Duffieux, op. cit.
|
|
Précision (anecdotique), Duffieux a un peu emmêlé les citations: c'est "à bas Euclide!" qu'avait lancé l'enfant terrible de Bourbaki, et la formule, prônant une nécessaire révolution de l'enseignement, avait fait florès (pas toujours bien comprise, hors de son contexte), jusqu'à Léo Ferré la transformant en "il faut mettre Euclide dans une poubelle!". Dieudonné s'en était pris, et avec raison, à l'excès d'exercices stériles qui ne regardaient que le nombril d'un triangle, marque d'un passéisme à enterrer.
Comment cela fonctionne-t-il?Qu'est-ce qu'un planimètre?Imaginez que vous faites un tour complet du périphérique parisien. Fun, non? Pourriez-vous en profiter pour donner sa longueur? Bien sûr: le compteur kilométrique de votre voiture fait très bien ça pour vous. Pourriez vous en profiter pour calculer aussi la surface de Paris intra muros? Cela poeut vous sembler bien moins naturel, mais, en gros, la réponse est oui, à condition bien sur d'adapter le mécanisme de votre compteur à cette tâche. C'est très exactement ce que fait un planimètre: en parcourant un contour (sur une carte d'échelle connue), il fournit la surface qu'il délimite. L'objet est donc d'une grande utilité, en particulier pour le cadastre... et les vendeurs de peaux de bêtes, mais oui, car l'objet vaut d'autant plus cher que sa surface est grande!
Pour celui qui a fait un peu de calcul intégral, le mystère sera moins dans les mathématiques, puisque la machine exploite la formule de Green-Riemann, qui relie l'aire à une "promenade" le long du bord, que dans l'habileté mécanique à faire en sorte que le dispositif produise, à chaqque instant, une quantité proportionnelle à y.dx -il n'y aura plus alors qu'à les sommer au fur et à mesure Pour les autres, on peut proposer un modèle approché, mais simple, qui lève ce mystère. <à
venir>
Comment devient-il un analyseur harmonique?L'appareil d'Amsler est
très simple et surtout peu encombrant, ce qui en assure le succès: il
se compose de deux bras; à l'extrémité de l'un, la pointe sèche qui
décrit la courbe; à l'extrémité de l'autre, un point fixe -d'où son
nom: la courbe apparaît comme tracée en coordonnées polaires d'origine
ce point. Disques et roulettes de calcul sont logées dans son bras.
|
 |
|
| Jakob Amsler (1823-1912) |
son planimètre polaire (exposition Prendre l'aire, Musée des Arts & Métiers (Paris) |
L'adaptation, bien visible
ci-dessous et à gauche, consiste en l'ajout d'une sorte de pantographe
à support triangulaire, à la pointe duquel se trouve un triaingle
rectangle mobile autour de son sommet, et un ensemble crémaillère -roue
dentée. C'est en changeant a taille de celle-ci qu'on changera de
coefficient de Fourier!
 |
 |
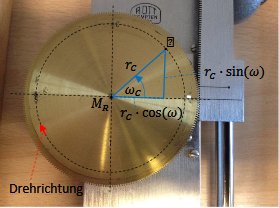 |
| de gauche à droite: le planimètre, la crémaillère et sa roue dentée, le pantographe |
la pointe sèche suit le tracé de la fonction f |
la roue dentée a une taille adaptée à l'harmonique étudiée |
L'idée revient en gros à ceci: tout se passe comme si, pendant que l'on suit le tracé d'une fonction f , le système pantographe-crémaillère-roue dentée communiquait au planimètre un mouvement similaire à celui qu'il effectuerait pour calculer l'aire correspondant à l'intégrale de Fourier du n-ième coefficient; On passe du cosinus au sinus en changeant le point d'attache et on change d'harmonique en changeant d'engrenage. Le calcul détaillé avec les figures explicatives (ne retenant que les parties géométriquement utiles de l'appareil) se trouve dans cet article.
Voir une autre description et une explication complète illustrée sur son fonctionnement, et une notice d'époque (en Allemand). Il est également brièvement décrit, avec une photo du coffret, dans cet article sur les analyseurs mécaniques.
Tout ce que vous voulez savoir sur les étoiles...
sans y avoir jamais mis le pied!
L'idée que l'on puisse acquérir des données de tempérarure, de composition chimique, de vitesse d'objets extrémement éloignés par la seule étude de spectres vous semble bien peu intuitive?
Mais c'est une réaction très saine! Cela n'a rien d'intuitif, mais
qu'on puisse y arriver fait partie, non des mystères, mais des beautés
de la science. Si vous êtes pressé d'avoir une première idée, ou si
vous voulez ensuite retrouver un point de référence, consultez cette page du site Culture Sciences Physique (site de vulgarisation de l'ENS Lyon).Prélude Chimique: faire parler un Spectre...
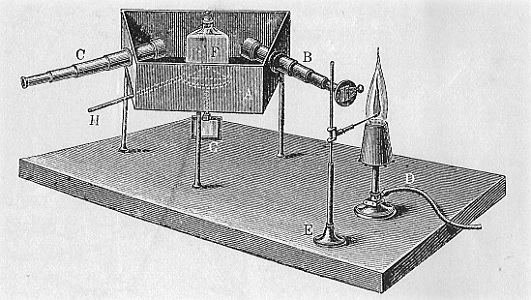
Quelle lumière émet un corps chauffé, quelle lumière absorbe-t-il? C'est en 1859 pour Bunsen et Kirchoff un nouvel angle d'attaque plein de promesses pour l'analyse chimique; ils construisent à cette effet le premier spectroscope. Une lunette pour éclairer, une pour observer, et entre un prisme pour disperser la lumière, pas encore de transformée de Fourier à l'intérieur, visiblement! Vous trouverez leur article et un commentaire de lecture sur BibNum. La figure ci-contre montre clairement, à partir de la dispersion classique de la lumière blanche par le prieme (Newton), les raies d'émission d'un corps chauffé, et les raies noires d'absorbtion du corps froid: ce sont les mêmes, et donc la réunion des deux spectres est le spectre complet de la lumière blanche. Ils proposent ainsi une interprétation des raies noires de Fraunhofer dans la lumière solaire, ouvrant par là même une voie royale de l'astrophysique: |
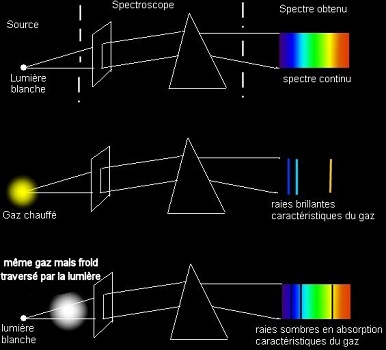 cliquez pour agrandir! (source: Wikipedia) |
|
|
||
Fourier fait son entrée... naturellement!
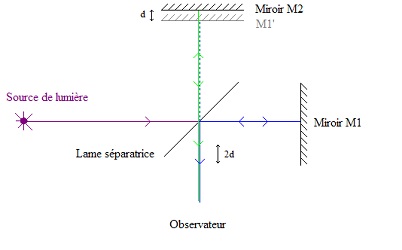
Dans les cas précédents, les physiciens étaient aller chercher un outil qu'ils connaissaient par ailleurs -la série de Fourier- comme on va en chercher une pince ou un tournevis dans son atelier: "si j'essaye avec celui-là, ça ira peut-être mieux...". Ici, changement de registre: non seulement c'est l'intégrale de Fourier qui intervient, mais c'est la mise en équation du problème qui la fait apparaître.Tout commence avec un célèbre appareil, l'interféromètre de Michelson, que l'on trouve décrit un peu partout (voir par exemple cette animation):
un rayon est divisé en deux de façon à pouvoir interférer avec
lui-même. La différence de marche, source une fois de plus des
interférences, est réglée par le déplacement d'un des miroris
réfléchissant (M2, sur ce schéma emprunté à l'article de Wikipedia);
elle produit des franges claires et sombres, voire colorées si la
source n'est pas monochromatique, ce qui va nous intéresser.
Tous les spectromètres à transformation de Fourier, des modèles héroïques des premiers temps aux appareils les plus récents embarqués pour des missions d'exploration spatiale, incorporent ce dispositif. |
 |
En notant x la différence de marche (ce qui revient à prendre pour le déplacement du miroir d=x/2), un faisceau monochromatique incident de longueur d'onde λ , d'intensité lumineuse I produit pour l'observateur une intensité de sortie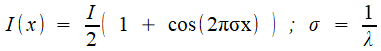 Une source polychromatique est caractérisée par sa distribution spectrale S(σ), qui donne sa densité d'énergie selon la fréquence; et c'est celle-ci qui intéresse les astrophysiciens, parce qu'elle va les renseigner sur la composition chimique des atmosphères des étoiles et planètes: c'est là qu'on rejoint notre prélude chimique! Chaque "bande infinitésimale" de fréquence spatiale contribue pour S(σ) cos (2πσx) dσ, et l'on ontient l'intensité de sortie par une sommation, laquelle est réalisée par une intégrale puisque σ varie de façon continue: 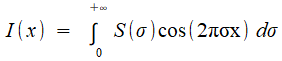 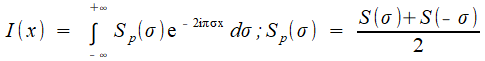 |
|
L'appareil ne donne pas accès directement à la quantité qui est l'objet de touttes les convoitises... mais à sa transformée de Fourier!
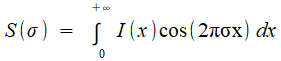
Le calculateur sera donc intégré à l'appareil pour fournir au chercheur les résultats en clair.
Spectrum ex Machina (en laboratoire)
Nous avions laissé plus haut un Duffieux redécouvert aux U.S.A. mais bien incompris en France... pas de tout le moncde, cependant. Lui, le pionnier... allait inspirer d'autre pionniers, mais dans le domaine de la spectroscopie astronomique... et l'introduction du calcul sur ordinateur:|
On s'est mis à jouer avec une autre possibilité. Par
le travail de P.M. Duffieux, on savait évidemment que les transformées
de Fourier intervenaient dans la théorie de la diffraction. On
dressa donc des plans pour enregistrer des interférogrammes sur une
plaque photographique [...] Le motif de Fraunhofer fournirait une sorte
de réponse. La méthode n'avait rien d'absurde, mais ne paraissait pas
franchement attravtive: telle était la Spectroscopie par Transformée de
Fourier, supposée prendre un avantage écrasant sur les spectrographes. [...]"
|
|
 IBM 650 (Wilkipedia) |  IBM 7040 (Wilkipedia)
|
|
||
|
||
Petit flashback
pour raconter comment cette équipe se constitua autour de Pierre
Jacquinot... de quoi faire éprouver un peu de nostalgie aux jeunes
chercheurs d'aujourd'hui! Voilà qui laisse une impression semblable à
celle d'un Didier Daurat recrutant avec le même flair des pilotes de
légende pour l'Aéropostale...
 |
"J'avais eu en 1956 ou 57, une idée qui
s'est révélée très fructueuse. Celle d'une nouvelle méthode de
spectroscopie appelée "spectroscopie de Fourier". Une des premières
choses que j'ai donné à Jeanine Connes, était de faire des expériences
préliminaires simples pour voir si l'idée était valable... Cela lui a
donné le sujet de sa thèse. Puis Pierre Connes s'est mis sur le sujet
et il a obtenu des résultats. Or il se trouve qu'une des
caractéristiques de cette méthode de spectroscopie, est de nécessiter
des gros calculs. D'où l'utilisation d'un ordinateur. C'était même
l'une des conditions essentielles de réussite de la méthode de
spectroscopie de Fourier. Il y a un autre coté, purement physique, qui
fait appel aux interféromètres. Il s'agit d'une technique très belle,
mais très difficile. Et petit à petit, madame Connes a été amenée à
s'intéresser à l'aspect calcul, mais en utilisant des ordinateurs qui
n'étaient pas au laboratoire. Si j'ai bonne mémoire, les calculs se
faisaient chez IBM, place Vendôme. Ensuite, on a utilisé les services
du Centre Blaise-Pascal, le centre de calcul du CNRS. Les ordinateurs
de l'époque étaient des clous par rapport à ceux d'aujourd'hui. Tout
cela explique que nous soyons devenus en quelque sorte des spécialistes
du calcul dit de Fourier."
"Connes est un monsieur un peu génial, physicien remarquablement imaginatif, très habile expérimentateur. Comment l'ai-je rencontré ? Il se trouve que comme beaucoup d'universitaires, j'ai été amené à faire parti du jury de l'agrégation féminine de physique. En 1952-54, il y avait encore une agrégation féminine. Après l'oral, les membres du jury reçoivent les candidats[...] Donc pour cette agrégation de 1954, je recevais les candidates, il y avait une certaine Jeannine Roux, épouse Connes. Elle ne devait pas être mariée depuis très longtemps, mais suffisamment pour être enceinte, elle s'était évanouie juste après sa leçon. "Qu'est-ce que vous voulez faire ? - je veux faire de la recherche. (j'avais eu une très bonne impression lors de sa leçon) - je peux vous obtenir un poste au CNRS dans le Laboratoire Aimé Cotton. - Mon mari vient d'être reçu lui aussi à l'agrégation, il aimerait bien pouvoir venir lui aussi (Il avait été nommé prof dans un lycée parisien). - Appelez-le si vous voulez, il bricolera au laboratoire. Et pendant un an, Pierre Connes est venu "bricoler" et il s'est révélé un chercheur de tout premier ordre. " |
Un expert en calcul de tranformée de Fourier, James Cooley -ni plus ni moins qu'un des deux inventeurs de la FFT (voir la page Fast and Fourier) a tenu à rendre hommage à Jeanine Connes dans un artcile historique retraçant sa découverte:
|
"Un des contacts qui s'avéra d'un grand bénéfice mutuel fut notre relation avec Jeanine Connes. Elle nous avait écrit la première, pour dire qu'elle avait à calculer des transformées de Fourier de très longues suites de données.
Il s'agissait de mesures d'interférométrie réalisées par un nouvel
appareil, plus puissant, mis au point par son mari, l'astronome Pierre
Connes. Un fait remarquable était que le calcul portait sur un seul
enregistrement d'environ 512 000 points, et toutes les fréquences du spectre étaient requises! Cela dépassait de loin la capacité des mémoires ultra-rapides de toutes les machines existantes [...]
Ces idées, jointes à un effort monumental de Jeanine Connes, aboutirent à son calcul du spectre infrarouge des planètes, qui a été publié dans un livre devenu une référence standard." |
 |
Avouons le, nous avons longtemps cherché en vain une image de l'héroïne... et puis, en rédigeant un article pour les actes d'un colloque d'histoire des mathématiques (Toulouse, mai 2022), l'obstination -encore vaine en préparant le diaporama de l'intervention!-enfin le gros lot... certes, elle est un peu cachée, à l'image de sa modestie, mais tout de même, les trois principaux protagonistes sonti ci réunis! Comment, il est vrai, pourrait-il en être autrement dans un colloque mondial sur le sujet, tenu à l'université d'Orsay en 1966? N'hésitez pas à consulter ce touchant hommage à Pierre Jacquinot, rédigé en 2007 par son fils.
au
premier rang, de g. à d., Pierre Connes, Pierre Jacquinot, Derek
Jackson, Jeanine Connes. |
Spectrum ex Machina (de l'Atmosphère aux Étoiles)
Quelques exemples seulement, pas une liste exhaustive: elle serait trop longue (et sans doute répététive). L'astronomie exploite tout particulièrement la partie infra-rouge du rayonnement.Depuis le Sol...
Les pionniers n'en sont pas restés aux échantillons de laboratoire, et
ont immédiatement tourné leurs spectromètres vers le ciel (au bout d'un
téléscope, bien sîr). Jeanine et Pierre Connes, avec Jean-Pierre
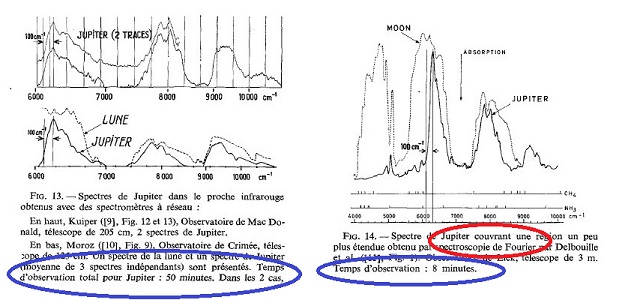
Maillard, montrent dès 1967 dans l'article Spectroscopie astronomique par Transformation de Fourier
les avantages qu'offre cette nouvelle technique en comparant, autant
sous l'angle de la qualité que sous celui du temps de calcul, les
sprectres obtenus pour Jupiter.
|

|
 | |
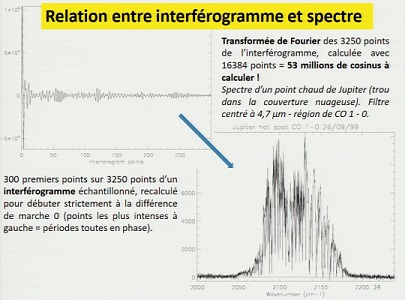 |
50 ans après (en 2017 donc), lors d'une conférence historique à l'Institut Astronomique de Paris, l'un des deux protagonistes de cet article, J.P. Maillard, donnait l'exemple du calcul nécessité par l'étude d'un point chaud du spectre de Jupiter en 1999: l'interférogramme était numérisé sur 3250 points, dont on avait calculé la transformée de Fourier sur 16384 valeurs: cela représentait 53 millions de cosinus à calculer et combiner! Que ferait-on sans la FFT... |
| ci-contre, la diapositive de la conférence évoquant ce calcul, montrant interférogramme et spectre. la flèche bleue... c'est la transformation de Fourier! |
 |
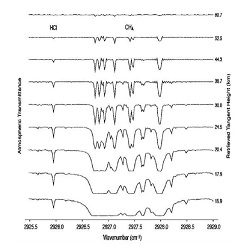
Idéalement située loin de la pollution, dans un air très sec, la Station Scientifique Internationale du JungfrauJoch (alt: 3450m), en Suisse, était dès 1950 équipée d'un spectroscope infrarouge pour l'étude du rayonnement solaire et de l'atmosphère terrestre, pour y détecter la présence de composés plus rares: CO, CH4,puis HCl, HF,... À partir de 1974 y est installé un spectromètre à transformée de Fourier dont la qualité technique permet l'étude de l'atmosphère au coucher et au lever du soleil. Un deuxième instrument y est installé en 1990; une vingtaine de composants peuvent y être surveillés en permanence, dont ceux qui, fort heureusement pour nous, ne sont présents qu'à l'état de trace, mais que le protocole de Kyoto a désigné comme gaz à effet de serre: hydrofluorocarbures, hexafluorure de soufre.. . Si l'on veut bien se souvenir que Joseph Fourier fut le premier scientifique à écrire sur l'effet de serre, la présence, 200 ans plus tard, des outils mathématiques qu'il a conçus dans des instruments sophistiqués d'analyse en dit bien plus long sur son rôle que bien des discours! |
... ou dans l'Espace!
 Source: Wikepedia et Nasa |
|
|
 |
 |
|
|
Vous brûlez d'en savoir plus sur les succès de la Transformée de Fourier dans l'étude des planètes et galaxies?
Vite, n'attendez plus! Après ces magnifiques débuts, la suite de l'histoire est à retrouvrer dans notre page spéciale: : Fourier, Vénus, Mars et les Autres : la FFT en missions spatiales, au service de l'Astrophysique, de 1977 à... l'actualité la plus récente.
MAIS... revenez après, pour ne pas louper la détection des exoplanètes: là aussi Fourier est de la fête! |
Dans un Synchrotron!
Dans le projet SOLEIL (CEA/CNRS, 2006; site web ici),
ce sont, à leur tour, les ultra-violets qui sont l'objet de l'attention des chercheurs. On
aura donc, au gré de cette page, parcouru tout le... spectre, sauf le
rayonnement gamma!
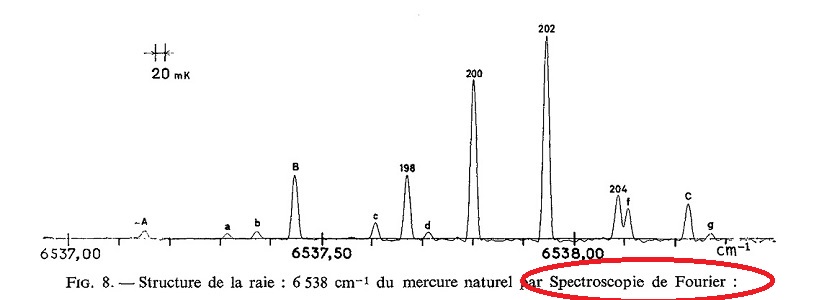
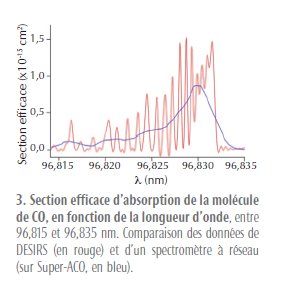
Il s'agit d'explorer l'infiniment petit, cette fois: la structure électronique des atomes et des molécules. Par exemple, les spectres des diverses molécules de monoxyde de carbone, selon les isotopes, ont pu être bien mieux précisés. Voir ce document, dont nous avons extrait les vignettes d'un spectre obtenu, et du spectromètre à transformée de Fourier. |
 |  |
|
|
||
Tout ce que vous voulez savoir sur... les exoplanètes (sans y avoir jamais mis le pied non plus!)
|
" La perle de l’astronomie qu’est la découverte des exoplanètes repose
sur l’analyse de Fourier des spectres émis par les étoiles."
Jean-Pierre KAHANE, conférence à l' École Polytechnique (10/05/2011)
|
La méthode employée est dite des vitesses radiales, et elle s'appuie sur un ingrédient physique fondamental, le célèbre effet Doppler. Bien connu pour les ondes sonores, où l'on perçoit comme plus aigüe la sirène qui se rapproche, et plus grave celle du même véhicule qui s'éloigne, il s'applique à toutes les ondes... tenez, sans vouloir fâcher aucun lecteur en lui rappelant le mauvais souvenir d'un instant de distraction, les ondes radar, par exemple... C'est dire qu'on peut en tirer une mesure de vitesse! Un examen médical a fait de ce nom propre un nom commun (On va passer un Doppler, entend-on souvent), et c'est encore une vitesse qu'on mesure, celle d'un flux sanguin, à l'aide d'ultrasons.
| Maison habitée par Doppler à Prague, et sa belle plaque souvenir |
Sa maison natale à Salzbourg (Autriche) |
||
 |
C'est en 1842, à Prague où il résidait depuis 1837, que Doppler écrivit
son article fondateur. Comme on peut le constater à son titre, il
pensait que cela permettrait de mettre en évidence des étoiles binaires
non reconnues par l'observation directe au téléscope. Dans un tel
système, les deux étoiles tournent autour de leur centre de masse
commun, donc la composante radiale de la vitesse (dans la ligne de
visée
terre-étoile) varie périodiquement, et il en résulte un décalage du
spectre de l'étoile par effet Doppler.
Pour une planète en orbite autour de l'étoile, le principe demeure le même: la loi de gravitation de Newton n'est pas universelle pour rien! Les deux tournent
encore autour du centre de masse de l'ensemble: l'étoile n'est donc plus tout
à fait immobile (ce qu'elle paraîtrait si elle n'avait pas de sattellite),.
Le problème est que la masse d'une planète est en général très
inférieure à la masse de l'étoile; donc la variation périodique, et
partant le décalage du spectre, sont plus faibles: cest pourquoi la
méthode ne réussit qu'avec des planètes assez massives, qui sont à leur
système ce que
Jupiter est à notre soleil (ce n'est donc pas un hasard si 51 Pegasi b
est quallifiée de Jupiter chaud).
|
| Le texte intégral dont la première page figure ci-contre est à télécharger ici; c'est une édition praguoise (en Allemand) réalisée pour le centenaire de l'auteur. |
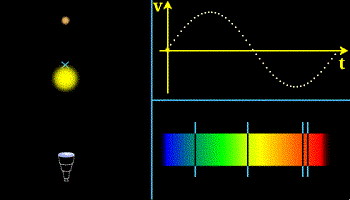
Vous verrez l'image ci-contre en version animée sur le site Culture Sciences Physique.de l'ENS Lyon. Quand vous y lirez:
"Le procédé qui permet d'atteindre de telles précisions sur les vitesses radiales consiste à enregistrer un large domaine spectral et d'utiliser simultanément environ 5000 raies d'absorption pour mettre en évidence le très faible déplacement de chacune des raies. Ceci fut rendu possible par les progrès de la spectrographie, des détecteurs et de l'analyse numérique des signaux." vous comprendrez que, sous ce que nous avons mis en gras, se cache la tranformée de Fourier, en version FFT, indispensable pour ces gros volumes de données ! |
 |
Toujours plus avec la Spectrographie de Fourier!
Et si, après ces voyages lointains, nous revenions un peu sur terre?Preuve s'il en est que la transformée de Fourier peut se consommer sans modération, elle se met désormais au service... de l'œnologie! Des spectroscopes dits "ITFR" (Infra-rouge à Transformée de Fourier) aident à l'acquisition très rapide et simultanée (30 secondes par échantillon) d'un nombre important de paramètres à surveiller dans le contrôle de la qualité: titre alcoolique, acidité totale (pH), acidité volatile, Sucres, acide malique… Voir plus de détails sur cette page de l'Institut Français de la Vigne et du Vin, ou cet article de la Revue Française d'Œnologie (n°208, Septembre 2004).
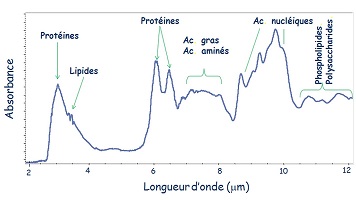 |
La miniaturisation des composants
sélectroniques et la baisse de leurs coûts ont fait ainsi passer dans
le domaine public des appareils qui étaient au départ l'apannage
excusif des laboratoires. Encore faut-il avoir une bonne raison de les
employer... Or, c’est dans la fenêtre spectrale du Moyen Infrarouge
(longueurs d'onde entre 2 et 20 µm, la bande IR complète s'étendant de
0,7 µm à 1 mm) que se trouvent les "signatures" des molécules
organiques constituant les tissus et fluides biologiques.
(L'exemple ci-contre provient de ce site). Lait et viande porcine ont été les premiers champs d'applications agro-alimentaires.
En savoir plus sur la spectroscopie ITFR. |
La Revue Française d'Œnologie souligne le "succès de cette méthode mise au point en France, et qui est maintenant appliquée dans le monde entier." Deux caractéristiques depuis longtemps partagées par le versant mathématique de l'Analyse de Fourier!
Références
- La Cristallographie décrypte la matière , Lettre de l'Académie des Sciences n°34 (2014)
- Exposition: Cristallography. Defining the Shape of Our Modern World (Univ. of OIllinois, Urbana-Champaign)
- C.A. BEEVERS, H. LIPSON, A Brief Histoory of Fourier Methods in Crystal-structure Determination (Aust. Journal of Physics, 1985, n°8)
- S. RAVY, Comment Fourier a transformé la Cristallographie (Conférence à l'Université de Caen, 2014; ses diapos de présentation)
- P.-M. DUFFIEUX, Comment j’ai pris contact avec la transformation de Fourier (Conférence Applications de l'Holographie, Besançon 1970)
- J. CONNES, Le Filtrage Mathématique dans la Spectroscopie par Transformation de Fourier (J. Phys. Radium, 1961, n° 22 -6)
- P. CONNES, Early History of Fourier Transform Spectroscopy (Infrared Phys. Vol 24, 1984)
- P. CONNES, Pierre Jacquinot and the beginnings of Fourier transform spectrometry (Journal of Phys.II , 1992)
- S.F. JOHNSTON, In Search of Space: Fourier Spectroscopy, 1950-1970
- J. LEQUEUX, Early Infrared Astronomy (Journal of Astronomical History and Heritage, 2009, n°12,2)
- J.P. MAILLARD, La Spectroscopie de Fourier en Astronomie: des Origines à nos Jours (Vidéo de la Conférence à l'IAP, Décembre 2017)
- N. de OLIVEIRA, L. NAHON, Le spectromètre à transformée de Fourier de la ligne DESIRS à SOLEIL (Reflets de la Physique, n°34-35)
- J-F PICARD, P. JACQUINOT, Entretiens avec Pierre Jacquinot (Journal du CNRS, Août-Septembre1989
- E. BRIGHAM, The Fast Fourier Transform and its Applications (Prentice Hall)
- S. DAVIS, M. ABRAMS, J. BRAULT, Fourier Transform Spectroscopy (Academic Press)
- M. DERRICK, D. STULIK, J. LANDRY, Infrared Spectroscopy in Conservation Science (The Getty Conservation Institute)
- H; GOLDSTINE, A History of Numerical Analysis from the 16th through the 19th Century (Spinger)
- J. KAUPPINNEN, J. PARTANEN, Fourier Transforms in Spectroscopy (Wiley)
Poursuivre...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Revenir à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Revenir à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique