 |
|
| Depuis l'église San Miniato al Monte, sur la rive sud de l'Arno. | L'octogone régulier du tambour est bien en évidence. |
Et pourtant, ces huit pans sont des cylindres elliptiques d'axe horizontal, ce qui n'est, déjà, pas si fréquent.
Mais le plus extraordinaire, c'est leur procédé de construction, qui fait -implicitement- intervenir des courbes gauches du quatrième degré! Des intersections de quadriques, comme vous en trouverez d'autres exemples dans nos pages dédiées. Cela passe totalement inaperçu sur place, et ce n'est que plus tard, lors de la diffusion ( 22/08/2014), sur la chaîne TV France 5 d'un documentaire: Le Duomo de Florence, mystère de la Renaissance (voir la bande-annonce), que le Mathouriste en a eu la révélation... à laquelle il vous convie à présent.
Des Cylindres Elliptiques, pourquoi?
La construction de la cathédrale Santa Maria del Fiore -puisque tel est son nom complet- débute en 1296: c'est l'aube de la Renaissance, et l'Art Gothique est encore dans sa phase "rayonnante" (1230-1350). Le Duomo conjugue donc une volonté de faire différent, de faire plus grand, tout en ne se dégageant pas complètement des techniques antérieures; la nef en est un exemple évident lorsqu'on y pénètre. Ainsi, l'idée neuve d'un dôme doit à l'antique (le Panthéon de Rome) et aux influences orientales (Istanbul), mais la construction va s'appuyer sur le principe de la croisée d'ogive, typiquement gothique. Celui-ci est parfaitement maîtisé, et emploie des règles empiriques comme celle "des quatre cinquièmes" (parfois "des trois quarts") qui positionnent les centres des cercles aux 4/5 (respectivement 3/4) du diamètre de l'arche. Ce principe est employé à Florence, et clairement matérialisé par les arcs de pierre qui constituent l'ossature du dôme, quatre croisées d'ogives située dans des plans verticaux, appuyées sur les sommets de l'octogone.Diapositive de Silvia Bertacchi, conférencce Domes in the World, Florence 2012
Entre
l'octogone (bas) qui définit le tambour, et celui qui, en
haut,
supportera la lanterne, se déploie un ensemble de
génératrices horizontales,
matérialisées
par la pose des tuiles du dôme extérieur, ainsi
que
l'alignement des petites ouvertures carrées. Sur chacune des
images, à droite, la réduction à un
point- ou
presque!- de chaque génératrice entre ses deux
extrémités de pierre offre une
deuxième
évidence visuelle.
Depuis le campanile de Giotto
Mais le mieux
pour s'en
convaincre... c'est d'aller voir ça du sommet du
dôme!
Nous avons matérialisé, sur celle de droite, les
génératrices comme lignes de pose des tuiles.
Depuis la lanterne
sommitaleLes petites coupoles de l'abside (à droite) reprennent le principe des huit cylindres du grand dôme (à gauche)
Ou encore, de l'intérieur: l'organisation des peintures décoratives s'appuie clairement sur des génératrices horizontales. Ceci dit, avec une petite tricherie sans conséquence: ce n'est pas le même dôme à l'intérieur, la coupole étant constituée de deux dômes emboîtés. Mais il est de la même forme, comme on le verra plus loin.
Quant
à la nature des
surfaces, elle est claire: les génératrices
ne font
un angle droit avec le plan de chacun des cercles; il ne s'agit donc
pas de portions de cylindres de révolution, mais de huit cylindres elliptiques.
Les ellipses, sections droites des cylindres, sont d'ailleurs
matérialisées par les escaliers qu'on emprunte en
effectuant l'ascension pour admirer la ville depuis la lanterne, du
moins, leur dernier tronçon. On a alors le dôme
intérieur pour plancher, et l'extérieur pour
plafond!
Dont acte, direz vous, mais on peut (presque) se passer de mathématiques pour ne pas se gâcher la vue après tant d'effort. (Presque) exact, mais pour que vous puissiez admirer cette coupole, ces peintures, et la vue depuis le pourtour de la lanterne, il a bien fallu que quelqu'un réussisse à la construire, non?
|
|
|
|
| d'après une coupe du National Geographic |
Une ascension indispensable:
outre la vue,
ce n'est pas tous les jours qu'on grimpe un escalier elliptique! |
sur une maquette en bois
(Museo dell' Opera del Duomo,
Florence)
|
Dont acte, direz vous, mais on peut (presque) se passer de mathématiques pour ne pas se gâcher la vue après tant d'effort. (Presque) exact, mais pour que vous puissiez admirer cette coupole, ces peintures, et la vue depuis le pourtour de la lanterne, il a bien fallu que quelqu'un réussisse à la construire, non?
Des Maçons... du Quatrième Degré!
Or, construire une coupole sans qu'elle s'effondre, ce n'est pas évident. À preuve, le cas de Sainte Sophie à Constantinople. Et quand on veut faire plus grand que tous les autres, le défi n'en est que plus grand, au point qu'il faillit ne pas être relevé! Et d'autant plus audacieux que ce dôme a établi un record de diamètre inégalé depuis, en dépit de gigantesques progrès dans l'ingéniérie des chantiers.Un Problème... Insoluble?
Dès 1315, l'essentiel de l'édifice est achevé, et le tambour octogonal prêt à recevoir la coupole dont les plans ont été dessinés. Là n'est pas le problème... le problème, c'est celui de la réalisation effective. De fait, l'église va rester plus d'un siècle inachevée, suscitant pêle-mêle des commentaires de désespoir, de furie et d'amère moquerie... Le mythe de Babel n'est-il pas en train de reprendre corps? L'homme n'a-t-il pas été trop présomptueux en lançant cette entreprise, fût-ce pour rendre hommage à la grandeur de Dieu? Dans les cités voisines d'Italie, qu'il s'agissait de surpasser en grandeur et en splendeur, les railleries sont, on s'en doute, impitoyables. La représentation dans la nef de son architecte principal présumé, songeur devant le plan de sa cathédrale, Arnolfo di Cambio (1240-1310), est largement postérieure, mais n'est pas sans évoquer cette perplexité...Pour sortir d'un siècle d'impasse, en 1418, un concours est lancé pour désigner celui qui, ingénieur autant que chef de travaux, se chargera d'édifier la coupole.
Techniquement, la méthode usuelle de construction ne peut être appliquée aux quatre croisées d'ogive qui structurent le dôme. Elle consiste, rappelons le, à poser les pierres sur un cintre en bois qui fait office de soutien temporaire, jusqu'à ce que l'introduction sommitale de la clef de voûte vienne, par le seul jeu de la répartition des forces de pesanteur, "caler" l'ensemble et permette de retirer le support de bois. Mais les dimensions de Santa Maria del Fiore l'interdisent; ou du moins, le coût d'une telle structure provisoire aurait été prohibitif, même au regard de la richesse de la ville: l'élever jusqu'à 90m au dessus du sol, partant d'un diamètre de 55m, exigerait d'énormes quantités de bois, et soulèverait des problèmes d'assemblage de ce support.
Sur ce point, tous les spécialistes, pourtant loin de s'accorder sur la solution victorieuse, sont unanimes: il a fallu édifier une structure autoporteuse, stable à toutes les phases de la construction du dôme.
Intermède Mathématique: Empliler des Morceaux de Sucre Il faut tout de même se défier des avis à l'emporte-pièce, du genre: "Il est évident que ça ne peut pas tenir!" Supposez qu'on vous pose la question: "Vous devez construire un surplomb en empilant des morceaux de sucre. Vous êtes libre d'utiliser autant de morceaux qu'il vous plaira -donc, la hauteur n'est pas limitée, mais jusqu'à quelle longueur pourrez vous vous avancer, en disposant vos sucres adroitement, sans qu'il y ait effondrement?" Il est probable que peu de gens donneront la bonne réponse, qui est: "Aussi loin que vous voudrez, il n'y a aucune limite!" tellement cela semble contraire à l'intuition première... La soultion, toute théorique, certes, repose sur la divergence de la série harmonique, c'est à dire le fait suivant: 1 + 1/2 +1/3
+ 1/4 + .... + 1/n
n'est pas
borné quand n
tend vers l'infini. Il suffit de disposer adroitement - très adroitement!-
les centres de gravité successifs pour résoudre
le problème... en théorie.(voir une solution détaillée ici, par exemple) En pratique, la réalisation s'avère ardue, pour ne rien dire de la fragilité en cas de réussite... Néanmoins, cet exemple peut nous aider à mieux comprendre qu'il est raisonnable de chercher tant que l'impossibilité physique n'est pas établie! |
Une précision s'impose: la coupole est double (voir l'image de l'escalier), le dôme extérieur s'appuie sur le dôme intérieur, qui est en briques. C'est de ce premier dôme, quasi invisible à la visite -sauf lors de la circulation dans les étroits escaliers d'accès au sommet- qu'il sera désormais question.
Un Orfèvre en la Matière... ou un Parfait Autodidacte?
Sa statue de
marbre veille jour et nuit sur son chef d'œuvre, sa
réussite indiscutée: pourtant, Filippo Brunelleschi (1377-1446) [
page plus riche,
en Italien] n'est, de formation,
ni architecte, ni mathématicien. Il est...
orfèvre, une
corporation florissante dans la ville qui sera, bientôt,
celle de
Benvenuto Cellini!
Face au Campanile de
GiottoComme
orfèvre, il a concouru en 1401 pour la décoration
des portes du célèbre baptistère
de la cathédrale. Et, malgré le -ou à
cause du?- style plus audacieux,
plus moderne de ses projets, il a "perdu en finale" contre Ghiberti. (Voir sur cette page leurs deux versions
du Sacrifice d'Isaac,
avec un petit film de comparaison, et une autre comparaison.)
Il n'est pas mathématicien, mais il sera pourtant l'un des premiers à comprendre la perspective centrale et à réaliser, en 1425, une expérience en illustrant les règles...avec, pour image, le baptistère Saint-Jean! (une video présentant son expérience)
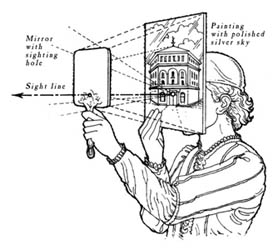
schéma de son expérience
Il n'est pas architecte, et pourtant, c'est lui qui va
gagner,
cette fois, pour l'édification du dôme.
Après son
échec de 1401, il est parti à Rome, où
il a
beaucoup étudié les monuments antiques, et
particulièrement le Panthéon et sa coupole de 43m
de
diamètre (Un monument à retrouver sur notre page Intersection
de Quadriques). C'était déjà beaucoup, mais la
hauteur du tambour était bien moindre; c'est ce qui avait permis aux
bâtisseurs du Panthéon l'emploi
d'échafaudages.
Il n'est pas mathématicien, mais il sera pourtant l'un des premiers à comprendre la perspective centrale et à réaliser, en 1425, une expérience en illustrant les règles...avec, pour image, le baptistère Saint-Jean! (une video présentant son expérience)
schéma de son expérience
Deux autres portaits
sculptés à Florence
Quand on lui demanda comment il
s'y prendrait, il refusa de le dire. On raconte (mais ce n'est
probablement qu'une de ces jolies légendes qu'on
écrit
après coup) qu'il aurait invité chacune des
personnes présentes à faire tenir un
œuf
à la verticale sur la table, et que tous
échouèrent, sauf lui, en cassant un peu
l'extrémité la plus large pour le poser
délicatement. Et de leur déclarer:|
«Vous dites maintenant que vous auriez pu faire la même chose. Sauf qu'aucun de vous n'a été capable de le proposer. Eh bien, si je vous dis ma méthode, vous pourrez construire vous-même la coupole!. » |
On
reconnait à cela... un génial
précurseur de
Christophe Colomb, à qui cette anecdote est le plus souvent
prêtée (sans qu'elle ait plus de
vérité
historique, d'aileurs). L'œuf de
Colomb aurait donc pu s'appeler l'œuf
de Brunelleschi!
D'un point de vue historiquement mieux étayé, il commença par se montrer ingénieux et innovateur sur les systèmes de levage des matériaux. Première innovation: une sorte de boîte à vitesse primitive, destinée à obtenir la montée et la descente des charges à partir d'un sens de rotation unique de l'axe moteur, entraîné par deux bœufs. Avant cette invention, il fallait dételer les bêtes, les réatteler pour les faire tourner en sens inverse, et additionnés, ces temps improductifs grevaient lourdement chaque journée de travail. L'inversion du sens de rotation de la roue verticale était produite par le simple fait d'engrener en partie haute ou basse.
Toutefois, il dut se résoudre, pour obtenir la confiance... et, très certainement, le financement des maîtres de la cité, à faire la démonstration de son système sur un "modèle réduit", récemment retrouvé lors de la construction d'un parking. (plus de photos grâce au quotidien florentin La Nazione)

source : [V1]
D'un point de vue historiquement mieux étayé, il commença par se montrer ingénieux et innovateur sur les systèmes de levage des matériaux. Première innovation: une sorte de boîte à vitesse primitive, destinée à obtenir la montée et la descente des charges à partir d'un sens de rotation unique de l'axe moteur, entraîné par deux bœufs. Avant cette invention, il fallait dételer les bêtes, les réatteler pour les faire tourner en sens inverse, et additionnés, ces temps improductifs grevaient lourdement chaque journée de travail. L'inversion du sens de rotation de la roue verticale était produite par le simple fait d'engrener en partie haute ou basse.
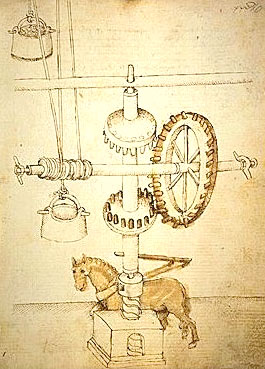
|
|
| source: www.infofirenze.com | palans employés lors de la construction. Museo dell'Opera del Duomo |
Toutefois, il dut se résoudre, pour obtenir la confiance... et, très certainement, le financement des maîtres de la cité, à faire la démonstration de son système sur un "modèle réduit", récemment retrouvé lors de la construction d'un parking. (plus de photos grâce au quotidien florentin La Nazione)
source : [V1]
Lorsqu'il
meurt, en 1446, la coupole est achevée, la
cathédrale
consacrée (1436), et la pose de la lanterne
commencée.
Mais il emporte dans son tombeau le secret de ses travaux.
Suprême honneur, il est enterré dans la crypte de
la
cathédrale.
Quand les Intersections de Quadriques œuvrent pour la solidité!
Brunelleschi n'ayant laissé aucun document, les historiens en sont réduits à des conjectures et tentatives de reconstitution de sa démarche, et le sujet a donné lieu à de nombreux débats, qui sont d'ailleurs loin d'être clos. Le chercheur le plus acharné sur cette question est sans nul doute l'architecte Massimo Ricci, qui a consacré une grande partie de sa vie à percer le mystère laissé par son illustre prédécesseur, jusqu'à entamer en 1989 la construction d'une maquette à l'échelle 1/5, dans un jardin public de la rive sud de l'Arno, le Parco dell'Anconella.Massimo Ricci justifie la démarche de son étude et de son expérience:
|
«Les modèles théoriques sont très intéressants pour appréhender la géométrie du dôme, mais d'une utilité limitée pour comprendre les problèmes qu'a dû affronter Brunelleschi pour le construire. Et ce qui m'interpelle vraiment, c'est la manière dont il s'y est pris pour assembler les briques. » |
Point de vue bien compréhensible, puisqu'il est architecte. Notre propos est néanmoins de montrer que, si sa théorie est exacte, la géométrie sous-tend le processus! Posons les règles dont nous partirons, en accord avec sa démarche, dictée par les impératifs techniques d'un chantier de l'époque:
- Postulat n°1: la coupole doit être construite par niveaux successifs de l'ensemble des 8 pans, globalement et non les uns après les autres.
- Postulat n°2: construire chaque niveau d'un pan par génératrices horizontales (qu'on empilerait chacune sur la précédente, à chaque tour) est irréalisable: sans cintre de soutien, la construction s'effondrerait.
- Postulat n°3: les seuls instruments "géométriques" pour guider le positionnement des briques sont des cordes tendues.
Travail de maçons à cordes tendues, sur le modèle de Massimo Ricci
(Captures d'écran des documentaires [V1] et [V2]cités en référence)
Commentons:
- le postulat n°1 reprend la technique de construction de tous les dômes depuis l'Antiquité (Panthéon de Rome, coupoles Sassanides...): on élève la coupole- de révolution- par cercles horizontaux successifs dont les rayons se resserrent progressivement jusqu'au sommet. L'adaptation stricte au cas du Duomo consisterait à construire des octogones successifs, se resserrant eux aussi; mais le postulat n°2 l'interdit!
- le postulat n°2 nous place devant un paradoxe: comment construire un cylindre sans le faire par ses génératrices successives? (Poser des briques en ligne droite est la technique la plus standard pour un maçon, qui emploie un cordeau)
- le postulat n°3 nous contraint à n'employer qu'une géométrie:
- de la règle et du compas, d'une part (droites par cordes tendues, cercles ou sphères par mouvement d'une longueur fixe de la corde tendue autour d'un point fixé);
- des surfaces réglées et des sphères.
Contrôle au cordeau des positions aux angles de l'octogone
(schéma de la revue BAC)
PB: connaissant le
positionnement des briques sur les cercles verticaux,
comment construire une portion de cylindre entre deux de ces positions?
Il en a déduit que les briques d'un niveau donné
ont été disposées en tendant
des cordes concourantes en un point de l'axe de la coupole.
Toutes ces cordes décrivent donc (virtuellement!) un
cône,
dont le sommet est donné par l'intersection des deux
premières génératrices connues, celles
qui passent
par les sommets de l'octogone. Ce sommet sert alors de point de
repère pour tendre les cordes suivantes, à partir
de la
courbe bordant l'octogone
-on reviendra plus loin sur celle-ci. comment construire une portion de cylindre entre deux de ces positions?
Massimo Ricci
pense avoir
découvert la solution en étudiant un document
ancien. Car
si Brunelleschi a pris soin de ne rien laisser... un de ses
adversaires, Giovanni di Gherardo da Prato,
a fait des figures très soignées,
dans le seul but de prouver que la méthode
échouerait!
Extraits d'une
animation du documentaire [V1] :
|
|
|
|
| départ: deux cordes issues des sommets de l'octogone de base, définissent le sommet du cône | à tout moment, ensuite, la corde est astreinte à passer par ce sommet et un point choisi sur la base. | le mouvement se poursuit... |
Soit, sur le terrain, dans la construction du modèle au 1/5 de Massimo Ricci
| Les génératrices du cône , matérialisées par les cordeaux tendus, donnent la position des briques d'une nouvelle rangée à disposer . ( [V1]) | |
et par suite:
Chaque ligne
de briques posée est , géométriquement,
l'intersection du cône des cordes avec le cylindre que l'on est en train de construire!
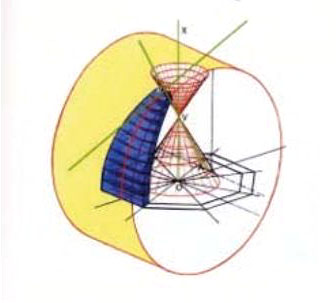
Intersection Cône (de révolution)- Cylindre elliptique, illustration de G. Conti dans [A2]
l'intersection du cône des cordes avec le cylindre que l'on est en train de construire!
Intersection Cône (de révolution)- Cylindre elliptique, illustration de G. Conti dans [A2]
Il s'agit donc, dans tous les cas (on discutera ensuite plus précisément la nature du cône) d'une courbe algébrique du quatrième degré, non plane, intersection d'un cylindre elliptique avec un cône du second degré. De deux quadriques, en somme!
Évolution des sommets des cônes en cours de construction
(d'après un schéma de la revue BAC)
Extraits d'une
animation du documentaire [V1] :
|
|
|
|
| Au fur et à mesure de la montée des murs, les sommets des cônes successifs s'élèvent le long de l'axe. | ||
| Oui! par couches successives de
courbes gauches... (Source: Associazione Filippo di Ser Brunellesco) . |
...ce
sont bien des cylindres
que l'on va construire! (état en 2011) (Source: Wikimedia Commons) |
C'est géométriquement plus inédit que de poser une génératrice sur une autre, mais beaucoup plus "rigidifiant" . Un échafaudage relativement minimal peut ainsi être utilisé sans qu'il ait à traverser tout l'espace vide sous la coupole.
Ceci dit, gare aux fantaisies et grossières inexactitudes que l'on trouvera aisément sur la toile!
Il est souvent dit, ici ou là, que ces courbes successives sont des chaînettes, donc optimisent la répartition des forces en adoptant la célèbre forme d'équilibre d'une chaîne pesante. Géométriquement, cette affirmation est fausse, pour au moins deux raisons:
- La chainette (ou caténaire) est une courbe plane, ce qui n'est pas le cas des intersections rencontrées ci-dessus,
- La chainette (ou caténaire) n'est pas une courbe algébrique, c'est à dire définie par des équations polynômiales; au contraire, les intersections de quadriques en général, et de cônes et cylindres du second degré, en sont.
Concédons que, sans doute, "plus on est proche" de la chaînette, plus la distribution des poussées est bien répartie. On peut sans risque l'affirmer du cercle par rapport à la droite, ce qu'ont compris intuitivement les bâtisseurs qui ont substitué la voute au linteau!
Il y aurait bien un prototype géométriquement et mécaniquement pertinent: la chaînette cylindrique, c'est à dire une courbe donnant la forme d'équilibre d'une chaînette pesante reposant sur le cylindre -ou, plus généralement, sur toute surface que l'on se donnera. Sa visualisation expérimentale est des plus simple à réaliser, et les bijoutiers y ont parfois recours pour présenter leurs colliers:
| |
|
| Les matériaux utilisés ont été choisis en écho aux goûts musicaux du Mathouriste : les
colliers sont d'authentiques colliers de Mardi Gras à la
Nouvelle Orléans, et le cylindre est ... suffisamment
auto-explicatif! Buddha (d'origine cambodgienne) a pour noble mission
de caler l'ensemble.
|
|
Car bien évidemment, Brunelleschi n'a écrit aucune équation, pas plus qu'il n'a eu l'idée de recourir à des intersections de quadriques. Il n'en avait d'ailleurs aucun besoin. C'est nous qui pouvons "relire" mathématiquement son ingénieuse méthode et l'interpréter géométriquement. Et s'il aurait pu réaliser au sol une maquette grandeur nature de chaînettes sur cylindre (avec une forme en bois), il aurait fallu reporter ensuite une bonne centaine de points par rang de briques: que de temps par rapport au déplacement d'une corde tendue!
Variantes de construction
Les films réalisés soulèvent toutefois une question. Alors que document de Giovanni di Gherardo (le voir plus haut à plat, sans effet de perspective) ne montre que des cercles circonscrits aux octogones, Massimo Ricci dessine ce quil appelle lui même une "fleur", formée de la réunion de huit arcs d'un rayon plus court.[V1] montre simultanément son modèle (cercle circonscrit) et son interprétation (fleur)
Rien n'est
dit -malheureusement- sur la motivation de ce choix (le document de
Giovanni di Gherardo
comporte-t-il d'autres précisions invisibles à
l'écran?). On peut donc imaginer les deux
possibilités,
et il semble bien que la première ait
été
envisagée par d'autres chercheurs et historiens. Disons
d'emblée que du point de vue
géométrique, ce n'est
qu'un détail mineur: dans tous les deux cas, le principe des
intersections cône-cylindre n'est pas remis en cause. Mécaniquement, cela aura sans doute plus d'importance!
Les figures suivantes de S. Di Pasquale, dont l'un des premiers usages à cet effet d'un dessin assis té par ordinateur, illustrent ce point de vue.
Pour les amateurs, les équations sont particulièrement simples à écrire.
Pour les constructeurs, sur le chantier, le contrôle reste certainement difficile, car il est impossible de matérialiser cet axe vetical qui "pend dans le vide". Les ennuis commencent avec le (grand!) cercle circonscrit, délicat à tracer puisque son centre est dans le vide!
Les équations sont un peu plus volumineuses, si l'on tient à les écrire; mais cela n'altère pas leur forme: les courbes sont toujours définies par l'annulation de deux polynômes du second degré. Ces courbes restent donc des intersections de quadriques.
On objectera, avec bon sens, que le centre du cercle constituant un pétale demeure, à l'évidence, "dans le vide". Mais son rayon est bien moindre (environ 12m, contre 25m à celui du cercle circonscrit): on peut aisément le construire au sol hors du monument, et soit préparer des fers courbes comme ceux de la maquette au 1/5, soit mesurer et reporter des distances perpendiculairement au côté du cercle circonscrit. On peut même le construire sur place, et à cordes tendues: c'est un petit jeu géométrique!
En voici la solution:
Cette construction géométrique a l'avantage d'être naturelle, immédiate et rapide, sur le chantier!
La courbe que forme alors le pétale est connue depuis l'antiquité: c'est la conchoïde de Nicomède (Elle est fameuse pour avoir été utilisée dans la solution du problème de la trisection de l'angle). Le mot conchoïde désigne une courbe obtenue par ajout d'une longeur fixe aux segments joignant les poinst d'une courbe "initiale" à un point fixe. Ici, la courbe de base est la plus simple possible (une droite), et le point fixe le centre de l'octogone.
Pour le mathématicien théoricien, un peu de changement: c'est une courbe dont l'équation est du quatrième degré. Il a naturellement tendance à la considérer comme plus compliquée qu'un cercle ou une conique (degré 2). Mais pour le maçon... ne sera-telle pas plus simple à construire, plus fiable qu'un cercle dont il n'a pas le centre? Comme quoi, avant de parler de simplicité, il est bon d'évaluer le contexte! La construction point par point n'exige pas de savoir former l'équation (D'ailleurs, l'argument est le même que pour le jardinier qui trace une ellipse, de degré 2, au cordeau...).
On n'a pas la certitude que Brunelleschi connaissait cette courbe. Elle existait avant lui, mais il peut l'avoir réinventée... il lui suffisait de se montrer ingénieux avec des cordes tendues, plutôt qu'habile à manier des équations. On n'a aucune preuve qu'il s'y est pris ainsi; de plus l'écart à un cercle bien choisi n'est pas nécéssairement énorme sur le chantier!
Un cône la prenant pour directrice aura lui aussi une équation du quatrième degré. La courbe modélisant une rangée de briques est alors une courbe algébrique du huitième degré, non plane, intersection d'un cylindre elliptique avec un cône du quatrième!
Surtout, il compare graphiquement et numériquement toutes les solutions: le point le plus important est la proximité mutuelle de la biquadratique et de la chaînette cylindrique. Et il conclut à un net avantage de la variante 1, à un seul cône de révolution, pour deux raisons essentielles:
Variante 1 : usage du cercle circonscrit
En ce cas, les cordes tendues pour chacun des huit murs appartiennent au même cône, et puisque celui ci a son sommet sur l'axe vertical de la coupole, perpendiculaire au plan de l'octogone, cet unique cône est de révolution.Les figures suivantes de S. Di Pasquale, dont l'un des premiers usages à cet effet d'un dessin assis té par ordinateur, illustrent ce point de vue.
Pour les amateurs, les équations sont particulièrement simples à écrire.
Pour les constructeurs, sur le chantier, le contrôle reste certainement difficile, car il est impossible de matérialiser cet axe vetical qui "pend dans le vide". Les ennuis commencent avec le (grand!) cercle circonscrit, délicat à tracer puisque son centre est dans le vide!
Variante 2 : usage de la "fleur" à pétales circulaires
Dans ce cas, deux différences sont à constater:- Pour une "rangée" de briques donné, il n'y a plus un, mais huit cônes, de même sommet, mais chacun ayant pour base un cercle différent (un pétale de la fleur);
- Ces cônes ne sont pas de
révolution: la droite joignant le sommet au
centre du cercle d'un pétale n'est pas perpendiculaire au
plan de l'octogone.
Les équations sont un peu plus volumineuses, si l'on tient à les écrire; mais cela n'altère pas leur forme: les courbes sont toujours définies par l'annulation de deux polynômes du second degré. Ces courbes restent donc des intersections de quadriques.
On objectera, avec bon sens, que le centre du cercle constituant un pétale demeure, à l'évidence, "dans le vide". Mais son rayon est bien moindre (environ 12m, contre 25m à celui du cercle circonscrit): on peut aisément le construire au sol hors du monument, et soit préparer des fers courbes comme ceux de la maquette au 1/5, soit mesurer et reporter des distances perpendiculairement au côté du cercle circonscrit. On peut même le construire sur place, et à cordes tendues: c'est un petit jeu géométrique!
En voici la solution:
|
|
|
|
|
||
Variante 3 : usage d'une "fleur" plus sophistiquée
Mais Massimo Ricci a imaginé une autre solution, toute en élégance géométrique. La vidéo ne la laisse pas deviner -ou plutôt, ne laisse pas assez de temps pour se rendre compte de l'idée. Voici une photo (de sa maquette) issue de son ouvrage [B4]: on y remarque que les cordesCette construction géométrique a l'avantage d'être naturelle, immédiate et rapide, sur le chantier!
La courbe que forme alors le pétale est connue depuis l'antiquité: c'est la conchoïde de Nicomède (Elle est fameuse pour avoir été utilisée dans la solution du problème de la trisection de l'angle). Le mot conchoïde désigne une courbe obtenue par ajout d'une longeur fixe aux segments joignant les poinst d'une courbe "initiale" à un point fixe. Ici, la courbe de base est la plus simple possible (une droite), et le point fixe le centre de l'octogone.
Pour le mathématicien théoricien, un peu de changement: c'est une courbe dont l'équation est du quatrième degré. Il a naturellement tendance à la considérer comme plus compliquée qu'un cercle ou une conique (degré 2). Mais pour le maçon... ne sera-telle pas plus simple à construire, plus fiable qu'un cercle dont il n'a pas le centre? Comme quoi, avant de parler de simplicité, il est bon d'évaluer le contexte! La construction point par point n'exige pas de savoir former l'équation (D'ailleurs, l'argument est le même que pour le jardinier qui trace une ellipse, de degré 2, au cordeau...).
On n'a pas la certitude que Brunelleschi connaissait cette courbe. Elle existait avant lui, mais il peut l'avoir réinventée... il lui suffisait de se montrer ingénieux avec des cordes tendues, plutôt qu'habile à manier des équations. On n'a aucune preuve qu'il s'y est pris ainsi; de plus l'écart à un cercle bien choisi n'est pas nécéssairement énorme sur le chantier!
Un cône la prenant pour directrice aura lui aussi une équation du quatrième degré. La courbe modélisant une rangée de briques est alors une courbe algébrique du huitième degré, non plane, intersection d'un cylindre elliptique avec un cône du quatrième!
Conclusion provisoire: Que choisir?
Un autre ouvrage, [B3], étudie la question, et il a le grand mérite d'être un travail d'ingénieur: si l'étude historique est loin d'être négligée, les solutions sont passées au filtre des calculs techniques des forces, des poussées. Son auteur, Jean-François Devemy, fait, lui aussi, énormément de dessins géométriques, mais les complète d'une étude mécanique quantitative totalement absente de celui de Massimo Ricci. Il envisage aussi la chaînette cylindrique, assimilée pour les calculs théoriques à une chaînette sur le plan tangent, mais qui sur le chantier pratique resterait la vraie courbe gauche, la corda blanda, cette corde détendue qui se "laisse aller" naturellement sur la surface, et il en confirme l'absence de maniabilité pratique, sauf pour vérifier que le lit de briques en reste proche.Surtout, il compare graphiquement et numériquement toutes les solutions: le point le plus important est la proximité mutuelle de la biquadratique et de la chaînette cylindrique. Et il conclut à un net avantage de la variante 1, à un seul cône de révolution, pour deux raisons essentielles:
- La plus simple des constructions sur le terrain donne des courbes très proches de l'équilibre naturel des lits de briques, ce qui justifie de ne pas perdre son temps à le rechercher d'une manière malcommode (de toutes façons approximative).;
- L'usage d'un seul cône par niveau offre, pour la solidité de l'édifice,
une continuité mécanique naturelle alors que les
solutions basées sur une "fleur" présenteraient des
fragilités aux angles. Tout en étant conforme à ce que l'on voit sur le document de Gherardo da Prato!
Quand les Loxodromies œuvrent pour la solidité!
Brunelleschi avait eu une deuxième idée pour renforcer la solidité: la pose de certaines briques "en arêtes de poisson" (spina pesce) pour créer des nervures fortifiant l'ensemble. Le simple décalage qui s'en suit, de rangée en rangée, crééait des courbes gauches (i.e. non planes) "s'enroulant" sur la structure, à la façon -apparente- d'un pas de vis.Par le choix du décalage d'une brique à chaque rang, assez intuitif eu égard à la solidité recherchée, les lignes de briques posées verticalement des courbes font un angle constant avec les lignes de niveau: c'est la défintion des loxodromies d'une surface.
Dans le cas des images ci-dessus, les courbes différeront selon que la coupole est sphérique, parabolique, ou de section droite une chaînette.
En ce qui concerne le vrai dôme, ou son modèle au 1/5, les courbes sont aussi des hélices, car elles font aussi un angle constant avec l'axe (horizontal) du cylindre. Insistons sur le fait que les deux types de courbes diffèrent sur une même surface (la sphère, par exemple), mais peuvent coïncider (le cas le plus simple, architecturalement étant celui des cônes et cylindres de révolution).
Il est malheureusement difficile de s'en rendre compte sur place, car on ne voit qu'un tout petit peu de la coupole intérieure en faisant l'ascension du dôme, et la conjonction des impératifs de sécurité: étroitesse des escaliers/ flux important de visiteurs ne permet guère de s'attarder en ces lieux. Mais les documentaires [V1] et [V2] les montrent clairement.
Sur ces courbes et leur occurence en architecture, le Mathouriste se promet d'écrire "prochainement" une page dédiée... Soyez patients et revenez nous voir!
Finir sur une petite Gourmandise:
De façon quelque peu inattendue, la même combinaison: cylindres elliptiques/ spina pesce se rencontre sur un monument antérieur (puisqu'il est du XIIéme siècle) dont il est peu probable que Brunelleschi ait eu connaissance. Il s'agit en effet d'une tour funéraire située dans la petite ville de Damâvand (Iran), non loin du légendaire mont éponyme et un peu à l'est de Téhéran. La similtude s'arrête là: le diamètre modeste du monument laisse penser qu'il n'a pas été difficile d'échafauder la coupole, et la spina pesce y joue un rôle purement décoratif, à côté de motifs autrement plus complexes. Cest le haut de la coupole qui est traité en réunion des huit cylindres, le bas étant simplement pyramidal. Mais cette forme de toiture est particulièrement rare dans la foisonnante diversité des tours funéraires qui parsèment l'Iran, et confère un cachet inédit à un monument dont on admire d'abord l'agencement décoratif des briques.Conclusion:
Quoique non terminé, le modèle de Massimo Ricci, édifié par des maçons professionnels venus tout exprès des USA -et qui se sont passionnés pour ce travail comme pour la découverte de celui de Brunelleschi- est particulièrement convaincant: cette manière de faire répond au problème d'une édification solide, stable à toute étape et n'ayant recours qu'à des échafaudages "raisonnables", sans pour autant compromettre la sécurité des travailleurs.Références:
Vidéos:
- [V0] How an Amateur Built the World's Biggest Dome, plaisant petit dessin animé, résumant bien l'histoire de la prouesse de Brunelleschi.
- [V1] Le Duomo de Florence, mystère de la Renaissance (voir la bande-annonce), diffusion France 5, Août 2014.
- [V2] Riddle of the Dome: Florence Cathedral and Filippo Brunelleschi (à voir intégralement ici) du National Geographic.
- [V3] Massimo RICCI, Conférence sur ses recherches relatives à la coupole, Florence, Palazzio Vecchio (09/11/2011).
- [V4] Luca GIOGI (Univ. de Florence) , Santa Maria del Diore, la Costruzione della Cupola, conférence à Alicante.
- [V5] Massimo RICCI, interview (2011): partie 1, partie 2, partie 3, partie 4.
Articles:
- [A1] Transcription de la vidéo [V2]
- [A2] Numero dedicato alla Cupola di Firenze, numéro Spécial du Bollettino Ingegneri, 59 (12). pp. 3-37 (2011).
- [A3] D. HUNT, Secret of the Duomo in BAC Journal, 2014/2 (revue de l'International Union of Bricklayers & Allied Craftworkers)
- [A4] M.-C. TORICCELLI, A Colloquio con Salvatore di Pasquale
- [A5] R. CORAZZI, La Curva “lossodromica” e la Spina Pesce
Livres:
- [B1] S. Di PASQUALE, Brunelleschi. La Costruzione della Cupola di Santa Maria del Fiore, Marsilio (2002)
- [B2] R. CORAZZI, G.CONTI, La Cupola di Santa Maria del Fiore raccontata da colui che l'ha progettata: Filippo Brunelleschi (Sillabe, 2005)
- [B3] J.-F. DEVEMY, Sur les Traces de Filippo Brunelleschi, l'Invention de la Coupole de Santa Maria del Fiore (Les Éditions du Net, 2013)
- [B4] M. RICCI, Il Genio di Filippo Brunelleschi e la Costruzione della Cupola di Santa Maria del Fiore (Sillabe, 2014)
Divers:
- Site du Congrès "Domes in the World", Florence 91-23/03/2012 (conférences disponibles en ligne sur inscription gratuite)
- Site de l'Associazione Filippo di Ser Brunellesco (née pour soutenir la construction du modèle au 1/5, présidée par Massimo Ricci)
- Site du Musée de la Cathédrale: Opera di Santa Maria del Fiore.
- Cupola del Brunelleschi, Wikipedia (page disponible en Italien seulement)
- Santa
Maria del Fiore, Wikipedia (et en Italien, plus
étendue)


